Linearized attention helps scale context length

Introduction
Attention mechanism has quadratic memory and compute complexity relative to sequence length. This factor makes it challenging to train long context models within a realistic time frame.
The main culprit behind this is the softmax operation used in the attention mechanism. This operation isn't decomposable, meaning that we can't break it down into smaller parts and then combine the results. If it was possible to replace softmax with something decomposable, we could potentially bring the attention down to linear complexity.
An example of a decomposable normalization operator is the ReLU function, which was used with cosine re-weighting in cosFormer (2022), producing a significant improvement in models trained from scratch. However, in case of modern LLMs, training foundation models that could match open-source vanilla alternatives like LLaMa, Mistral or Stable Beluga may not be feasible.
Thus, a function more similar to softmax is necessary, so that a model could adapt after abrupt continual pretrain.
Decomposable softmax alternative
The key non-decomposable operation in softmax is exponentiation:
exp(⊙QKT)
Our idea involves swapping this operation with:
exp(⊙Q)exp(⊙KT)
Mirroring arguments made by cosFormer (2022), for normalization to be successful, the needed properties are non-negativity and non-linearity, and our proposed change meets these requirements.
Now, by first multiplying the Keys by the Values matrix (resulting in a dxd matrix, where d is the feature dimension), it becomes possible to then multiply the Queries by the resulting matrix (Nxd by dxd, where N is the sequence length). This compuation has linear complexity relative to sequence length.
Vanilla attention on the other hand is bound to perform MatMuls in an more resource-intensive order: the final MatMul occurs between matrices of shapes NxN and Nxd. The operation is quadratic relative to sequence length as was stated earlier.
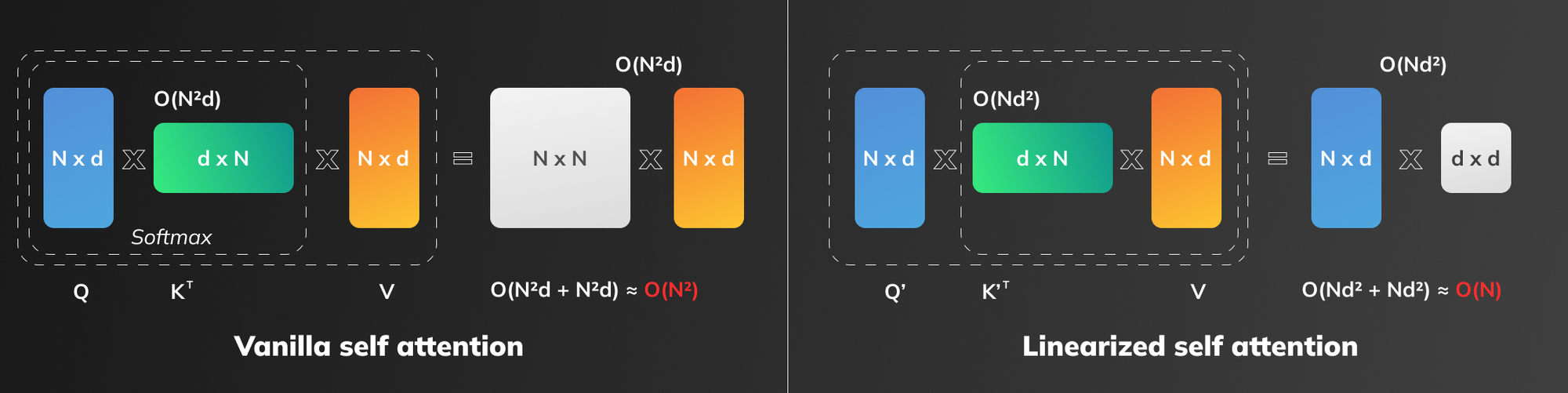
Figure 1 illustrates how the order of computations affects algorithm complexity.
In other words, our modification makes the algorithm complexity O(N) relative to sequence length.
This new approach also opens up the possibility of efficiently applying blockwise attention, where the query is broken down into more manageable chunks. Through this, we can cache K by V MatMul and sequentially process the final MatMul with all the chunks of Q, making attention memory constant.
Testing adaptability
We're currently in the process of testing these theories through the continual pretraining of a 7B LLaMa 2 model. The training was performed for 10,000 steps with each step consisting of 48,000 tokens, with an initial learning rate of 1e-4.
We see some compelling results. The model, trained on a randomly selected segment of the Slim Pajama dataset, achieved a training loss of 2.441.
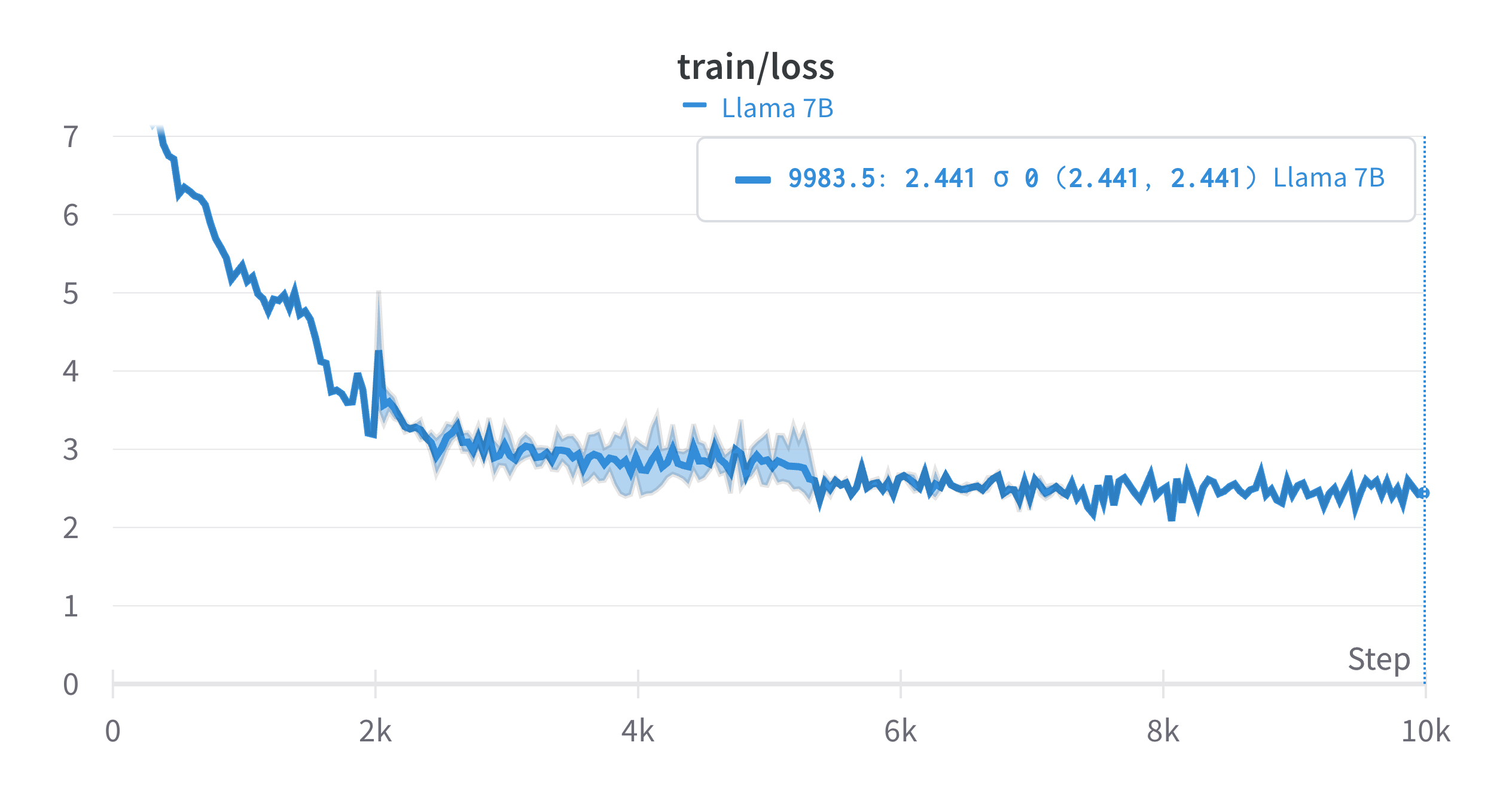
The learning curve from this experiment shows that our new softmax substitute has potential - the model certainly shows some ability to adapt. However, the loss value isn't quite where we'd like it to be yet.
Conclusion
The learning performance of our model demonstrates that the proposed softmax alternative is able to adapt to an extent. However, the loss value is not quite satisfactory. We are currently working on the extended experiment that would allow the model to see more tokens during adaptation.
